Ein neues geometrisch-physikalisches Grundgebilde
Teile meiner mathematischen Ergebnisse und ihrer physikalischen Deutung wurden auf der Pekinger Mathematiker-Tagung 2002
anhand eines Posters vorgestellt, das ich hier in der englischen Fassung wiedergebe und auf Deutsch erläutere.

1. TETRAGLOBE - eine konforme Grundfigur
1.1. Ich konstruiere die konforme Geometrie ohne Benutzung Euklidischer Elemente.
Eine solche autark entwickelte Geometrie bezeichne ich im Blick auf meine physikalische Deutung als "Natürliche Geometrie".
Die Welt dieser Geometrie kennt keine Geraden. Im Begriff "Konformkreis" sind die klassischen Begriffe "Gerade" und "Kreis" aufgehoben:
Ein Konformkreis ist kein Euklidischer Kreis, denn er besitzt beispielsweise keinen Mittelpunkt - ähnlich einer Euklidischen Gerade.
Ein Konformkreis ist niemals eine Euklidische Gerade, denn er ist immer in sich geschlossen - ähnlich einem Euklidischen Kreis.
Winkel sind Gebilde aus Konformkreisen, ihre Messung kann man nicht mittels Euklidischer Tangenten bewerkstelligen.
(Klaus Ruthenberg, Measurement of angles and elementary angle functions defined by conformal cross ratios,
Journal of Nat. Geometry, 18, 2000, 131-150; korrigierte Fassung in Jour. Nat. Geometry., 19, 2001, 73-92)
1.2. Ein Tetraglobe bildet die Basisfigur der Natürlichen Geometrie (Peking-Poster, Figur 1).
Jedes komplexe Doppelverhältnis ist als eine Maßzahl dieser Grundfigur zu verstehen.
Es gibt keine reellen Längenmaße, aber es gibt nicht-reelle Maßzahlen, die einen Tetraglobe metrisch beschreiben.
Diese Maßzahlen sind die Grundlage einer von der Euklidischen Geometrie (und ihrer Winkelvorstellung) unabhängigen Winkelmessung.
Ein Tetraglobe lässt sich auffassen als ein "nicht-euklidisches" Modell eines Euklidischen Dreiecks (mit Umkreis).
Es hat mit dem Euklidischen Dreieck gemeinsam die Euklidische Winkelsumme.
Die duale Struktur und eine viergliedrige Symmetriegruppe jedes Euklidischen Dreiecks treten erst auf der Ebene der Natürlichen Geometrie zutage.
(Klaus Ruthenberg, Conformal background of Euclidean geometry, Jour. Nat. Geometry, 19, 2001, 93-120)
Weil ein konformer Tetraglobe ebenso wie ein Euklidisches Dreieck im Wesentlichen nur genau drei Winkel besitzt (mit Euklidischer Winkelsumme),
spreche ich einen Tetraglobe auch einfach an als ein "(konformes) Triangel". Spätestens seit Hilbert ist jedermann klar,
dass zu unterscheiden ist zwischen der abstrakten Euklidischen Struktur und ihrer modellmäßigen, anschaulichen, physikalischen Darstellung.
Felix Klein war in der Lage, die Euklidische Geometrie als spezielles, metrisches System der Projektiven Geometrie zu verstehen.
Unsere physikalische Grundlagen-Diskussion krankt daran, dass eine analoge Betrachtung der Euklidischen Geometrie
vom höheren Standpunkt der Konformen Geometrie nicht bekannt (nicht üblich) ist. Ich führe dies unter anderem darauf zurück,
dass eine von der Euklidischen Geometrie unabhängige Konstruktion der Konformen Geometrie bis hin zum Winkelbegriff zum ersten Male
von mir durchgeführt wurde.

2. Ist das klassische Modell Euklidischer Dreiecke unzeitgemäß?
2.1. Hier in Übersetzung der Vergleich im Poster-Text
Noch in historischen Zeiten fassten menschliche Wesen ihre Erde als "flache Scheibe" auf.
Heute rasen - wie selbstverständlich - Satelliten um diesen Globus.
Seitdem Euklid seine Bücher schrieb, fasst die Mathematik seine 2-dimensionalen geometrischen Strukturen auf als Elemente einer "Ebene".
In meinen Augen ist eine Kugel der Natürlichen Geometrie (eine Konformkugel) das natürliche Darstellungsfeld für Figuren
der 2-dimensionalen Euklidischen Geometrie. Der Absolute Punkt, mit dessen Existenz man die Natürliche Geometrie
auf die Euklidische Geometrie reduzieren kann, kettet jede Euklidische Struktur an das Unendliche.
Der Absolute Punkt kann ersetzt werden durch individuelle Punkte, falls wir Euklidische Strukturen verstehen
als konforme Elemente der Natürlichen Geometrie.
(Klaus Ruthenberg, Measurement of Angles and Elementary Angle Functions
defined by Conformal Cross Ratios, J. Natural Geometry, 18, 2000, 131-150; korrigierte Fassung in J. Nat. Geom., 19, 2001, 73-92)
2.2. Die klassische Elementargeometrie entwickelt die Trigonometrie anhand Euklidischer Dreiecke und der Längen ihrer Seiten.
Zu ihrer Entwicklung ist jedoch bereits ein (rechtwinkliger) Tetraglobe hinreichend.
Auf diesem Wege ist es möglich, den Winkelbegriff als fundamental (primär), den Längenbegriff als sekundär aufzufassen.
Man hat zwar seit Entdeckung der Nicht-Euklidischen Geometrien gelernt, die Euklidische Geometrie von höheren Standpunkten zu betrachten.
Aber nirgendwo finde ich eine Entwicklung der Euklidischen Geometrie, die zunächst den Winkelbegriff und seine Trigonometrie
auf konformem Level einführt, um erst danach auch einen Längenbegriff zu definieren.
Dabei sollte beachtet werden, dass wir geometrisch-physikalisch zwar ein absolutes Winkelmaß (den Vollwinkel = 4 R),
aber kein absolutes Längenmaß besitzen. Physikalisch setzt die Längenmessung die Existenz starrer Körper voraus,
an denen Längenmaße abgenommen werden können. Starre Körper existieren aber in der Mikrophysik nicht;
sie existieren auch nicht in großen Bereichen der Astrophysik. Wieso kann man Theoretische Physik auf einen Begriff gründen,
der in weiten Erfahrungsbereichen nicht existiert?
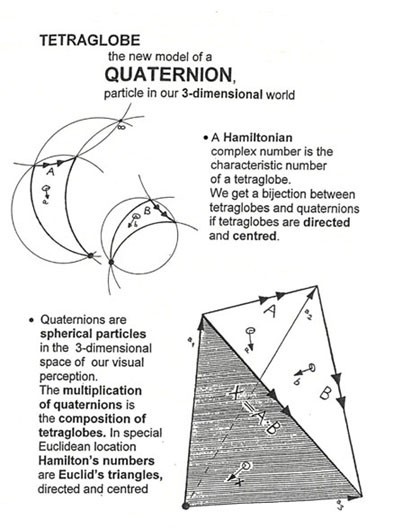
3. TETRAGLOBE - ein neues Modell komplexer Zahlen
3.1. Die klassische geometrische Auffassung der Zahlen führt zu einer merkwürdigen Lücke zwischen den ("2-dimensionalen") Komplexen Zahlen
und den ("4-dimensionalen") Quaternionen.
Meine geometrische Auffassung jeder Zahl als Tetraglobe ...
- befreit uns von einer Verabsolutierung des klassischen Punktmodells (Vektormodells) der Zahlen.
- macht klar, dass unsere Zahlen geometrisch im Wesentlichen nicht eine Euklidische, sondern eine rein konforme Struktur haben.
- führt zu einem geometrischen Bild der Quaternionen und ihrer Multiplikation im dreidimensionalen Raum unserer Anschauung.
(Klaus Ruthenberg, The quaternionic structure of 3-dimensional Natural Geometry, 16, 1999, 125-140)
3.2. Befreit man sich von der Punkt-Auffassung, so bekommt jede Zahl ihre individuelle geometrische Struktur.
Die Zahlen sind ähnlich zu denken wie physikalische Partikel im physikalischen Raum unserer Erfahrung.
Ohne Existenz eines längenmetrischen (kartesischen) Koordinatensystems haben sie zwar bereits eine wohl definierte innere (Winkel-)Struktur,
aber keine definierte Größe und keinen bestimmten Ort.